
The permanent location of this page is http://www.goban.demon.co.uk/go/bestiary/zippersetc.html
Contents:
I was looking at the Ing Rules, and became interested in Multistage Kos. Multistage Kos are Kos which lead to kos, which lead to kos, ... Simple ones -- 2-stage, or even 3-stage kos happen quite often in normal play, but I especially wanted to find completely implausible arrangements of ko captures which could go round in circles. Eventually, I was successful -- I found both Wheels and Loops, and on the way described extensions of various well-known Multistage Kos, and discovered/invented a few others, such as Trains, Split Zippers, and Crossing Zippers.
These notes are still incomplete, and date from early 1996. I supplemented them extensively with work done in October 1997, because I then "solved" two new (for me) classes of problem. In May 2000, I added a number of SGF files, corrected some minor errors, and added some extra material -- especially a reference to Berlekamp's Zig-Zag Zippers.
In all that follows, I have concentrated on looking at positions, and moves in them, that are 'legal' rather than 'sensible'. There will be many positions where one of the players might get a better result by playing differently -- obviously such a move would be 'sensible', however I have usually asked only if their move was legal -- i.e. obeys the rules of Go.
One of the next areas to be examined carefully should be to see if 'sensible' versions of all, or most, of the interesting 'legal' positions can be devised.
When I started looking at Multistage Kos in early 1996 I was already familiar with what I now call single-line zippers. I call these objects 'Zippers', since they can be open/closed, and can (normally) travel in either direction. I have found various types -- the basic categories are:
As some other people will probably have already done, I identified two distinct types -- one being a diagonal zipper, and the other being a linear (up-down or left-right) zipper.
The linear zippers travel parallel to the edges of the board.
The basic linear zipper that I found looked like this:

1996/1/30 HF
Note: This Multistage Ko I call a
'linear' 'zipper'. It is
bounded at each end by groups of
different colours. In this zipper
the ends are 'blocked' -- when Black
captures the last ko at the right of
the board, if Black does not connect
then White can eventually start
re-capturing and bounce back. The same
applies to White at the left-hand end. The
ends of some zippers may be 'open' -- if
a player makes a final capture which
cannot be undone. e.g. if the White
stone at S15 (the one in the middle of a
vertical row of three, 3 rows below the
top edge, and one line in from the right
edge) were Black (or empty) then Black
could make a capture at R14 (to the left
of this) which would
give Black control of the Right-hand as
well. Black would then not need to make
any more moves to protect against White
re-capture.
Clearly either end may be either blocked or
open independently of the other. This gives
rise to three different types -- open/open,
open/blocked, and blocked/blocked. Only the
last of these is like a real-world zipper
which is not broken.
Please note that in this zipper there is only
one white segment and one black segment. If
there were more than one of each then we would have a
Train.
We might call the linear zipper above a linear 8-zipper, to indicate that the maximum number of distinct ko captures for Black (or White) is 8.
This type of 'zipper' is extended later to go round corners, and eventually to create a 'square' wheel.
Most of us will be familiar with (smaller
versions of) the diagonal zipper:

1996/1/30 HF
The above diagram shows a 'diagonal' 'zipper' -- this one
bounded/bounded -- i.e. bounded at each end by a different colour.
As in the 'linear' zipper, in the example above, we can also
have the other two variants -- bounded/open and open/open.
We might call the diagonal zipper, above, a diagonal 7-zipper to indicate that Black (or White) can make a maximum of 7 distinct ko captures.
This type of 'zipper' is extended later to go round corners, and eventually to create a 'diagonal' wheel.
In the examples above we can see that:
There is yet another type of zipper, which I call a Zig-zag Zipper. In March 2000, Elwyn Berlekamp showed me some (then) unpublished work that he had been doing on the thermography of Multistage Kos -- I then realized that I had missed this family of Multistage Kos. Here is the example which he showed me:

Is it possible to create a bigger one on a 19x19 board?
If you want to play with this position then check out the SGF file.

1997/10/14 HF
In the diagram above there are 5 distinct segments
-- three white ones, and two black ones. We have
alternating White and Black segments or 'Trains'.
Simple zippers have only two segments, whereas the simplest
train has three segments.
Please note that when we continue capturing we enlarge one segment (at the expense of the one of the opposing colour which we are eating into). If we carry on doing this, and we join up with a train of our own colour then the two trains permanently become one, anihilating the 'gap' between them, and reducing the total number of segments by two.
Sensible use of multiple trains will prove essential if we want to make full use of the 'loops' and 'wheels' that we will discuss later.
At any given point along the length of a zipper, the two outer sides can be clearly distinguished from each other (irrespective of who has made the internal captures). This property I will call 'handedness', or chirality.
The chirality of a linear zipper may change along its length.
These properties can be used in building seemingly complex structures.
The above points are illustrated here:
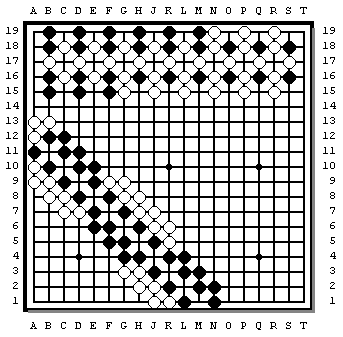
1997/10/21 HF
Note: In the horizontal linear zipper at the top
it starts at the left by being Black on both
sides; changes colour on one side; and then
changes colour on the other to become White
on both sides. In diagonal zippers we cannot change the
colours on either side independently, without destroying
the zipper. Please observe that the centre
line of the linear zipper is completely unchanged,
whereas when the outside of the diagonal zipper
at the bottom left changes colour there is an
apparent shift of line.
Later, when we join zippers together, there will be some combinations for which there exist two variants that are mirror images of each other, and thus 'handed'.
In the section on Split zippers we will see examples where it is possible for a player to move in one direction around a corner whereas they cannot move in the opposite direction. The other player may (or may not) be affected, and if so not necessarily in the same way. This displays another type of asymmetry in an otherwise seemingly 'simple' junction.
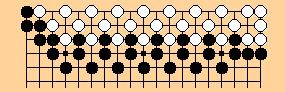
Linked linear zippers are like single linear zippers except
that they 'move' more slowly -- an n-wide linked
zipper moves at 1/n of the speed of an ordinary
zipper. A twin (or 2-wide) linked zipper moves at half the
normal speed because one has to capture in each
of the parallel linear zippers in turn:
1996/1/30 HF
A relative of this linked zipper is another twin (2-wide)
linked linear zipper:

1996/1/30 HF
or, almost equivalently, the twin linked
linear zippers:
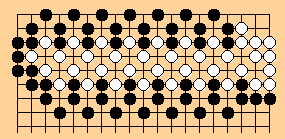
1996/1/30 HF
We could obviously have a mixture of the above 2 styles.
Here is an example of a twin (2-wide) linked diagonal
zipper, where the zippers are inter-connected
all the way :

1997/10/14 HF
There is also
an SGF version of this diagram.
The characteristic of an ordinary Double Ko, is that there are two kos. When Black wins either ko they get the same result -- to live a Black group, or to kill a White group. When White takes one ko, Black takes the other; when White finishes one ko, then Black finishes the other -- guaranteeing a successful outcome for Black. Using normal Double Kos, a group may live using a variety of methods -- by obtaining a second eye; connecting to another live group; connecting two groups to make one live group securing a mtaching eye in a seki; obtaining comparable liberties in a seki. It seems probable that most of these situations can be paralleled with multistage kos -- any offers?
We can form a sort of Pseudo Double-ko by joining together two one-line zippers. They do not have to be immediately adjacent. Neither do they have to be parallel to each other. Furthermore, they could even be of different types -- linear and diagonal.
Using single linear zippers, we might have:
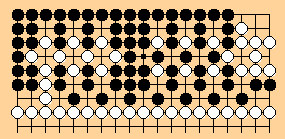
White to Play
1996/1/30 HF
Note: This can be cleaned up a bit.
Other possibilities exist, such that
the sequence of captures at left (or
right) is equivalent to a single ko --
i.e. each capture creates only 'half'
an eye, and certainly not multiple
eyes -- see the joined twin linear
zipper below.
This is the situation in the traditional
double ko, as well as the diagonal
zipper pseudo Double ko, below.
By joining two twin linear zippers -- end-to-end,
we get:
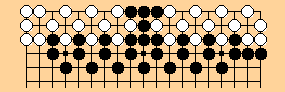
1996/1/30 HF
Joining diagonal zippers end-to-end, we might
have another diagonal zipper pseudo Double ko:

1996/1/30 HF
It seems very likely that the above ideas can be generalized to
create pseudo versions of triple-ko, quadruple-ko, ..., n-tuple ko.
Has anyone got time to do this?
Please do not confuse the above, joined, single-line, zippers with twin- (generally 'n-') linked single-line zippers -- they are completely different in character.
As well as the single-line zippers, and their linked versions, we have collections of zippers which have one shared end, and two, or more, other ends -- these I call 'Split' zippers.
In these it is possible to move (almost) independently in each 'branch'.
It is also possible to move down a branch to the shared end, and then travel out on another branch.
The sorts of simple joints/splits that we would like to create are:
| | / ( \ | ) \ / \ ( / ) |__ , |/ ( \| ), \/ , \___ ( ___/ ) ,(ignoring the chirality mentioned earlier).
All of these are possible, and are illustrated repeatedly, as part of more complicated configurations, later. Some versions of some joints are selectively 'one-way' -- e.g. Black may move both clockwise and anti-clockwise, whereas White can move only clockwise -- see later.
Furthermore we might want to use these to create some 3-way branches such as:
| / \ | / \ / \ | / \ | / \ / \ |/__ , \|/ , ___\/ , ___\___, etcseveral of which are illustrated below.
Additionally, from these, we might hope to create variegated 'crossing' zippers such as:
| \ | \ / \ | /
| \ | \ / \ | /
_____|_____ \| \/ \|/
| |\ /\ /|\
| | \ / \ / | \
| | \ / \ / | \
which, along with others, are shown in the section
on
crossing zippers.
In principle, we could create any 4-way, 5-way, 6-way, 7-way, and 8-way branch as well. Most of these have been left as an exercise for the reader, while some are shown later.
The crossing zippers are used in the creation of 'Loops' which are discussed later.
Here is an example:

1997/10/14 HF
Here is an
SGF version of the above diagram.
Note: A (horizontal) linear zipper, and a diagonal zipper meet, and in some sense are joined, at the branch point at the top-left of the diagram.
Note: White can travel round the junction in an anti-clockwise direction only, whereas Black can travel in a clockwise direction only. We do not seem to be able to change this property simply by making either (or both) of the zippers wider - i.e. twin linked zippers.
The mirror image of the 2-branch zipper above, clearly has a different handedness.
Here are some simple junctions at right angles:

1997/10/14 HF
Note: at the top we have two closely related
examples of two diagonal zippers meeting --
the example at the top left can occur only on the
edge.
In the bottom left we have two linear zippers meeting.
The diagram below illustrates some of the restrictions
on the movement by players at a junction -- in this case
some simple meetings of single linear zippers.

1997/10/17 HF
Here is an
SGF version of the diagram.
Note: In the Top Left, Black may travel round the corner in either direction, whereas White may go only anti-clockwise. In the Bottom Left corner, again Black may go in either direction (and in going round anti-clockwise may be able to "break" the zipper by making a double capture), whereas White may go only clockwise. Clearly we can have Black restricted, and White free, simply by reversing the colours in the diagram. In the Top Right, either player may go in either direction, whereas in the Bottom Right Black only may travel through the corner in either direction -- breaking the zipper.
We can extend the idea of a 2-branch zipper by
increasing the number of linear (and/or diagonal)
zippers, by linking them. For example we might do:

1997/10/14 HF
Note: twin linked (horizontal) linear zippers, and a
diagonal zipper meet at the branch
point at the top-left of the diagram.
Black can travel clockwise (only), whereas
White can travel anti-clockwise (only). There is
an SGF version of the file
to experiment with.
or, even worse:

1997/10/14 HF
Note: twin linked linear zippers, and twin
linked diagonal zippers meet at the
branch point at the top-left of the
diagram. We have
an SGF version of the file
to experiment with.
And here is an example of a 3-branch zipper:

1997/10/18 HF
Note: White can travel in neither
direction round any part of the joint.
Black, however, can travel round the
joint only if going vertically upwards
to start with -- Black may then go either
to the left or to the right.
Here is another 'arrow' shape:

1997/10/18 HF
Note: Both players' movement is restricted in
moving round the joint. They can go down the
diagonal and then out on either branch, but
cannot do the reverse unconditionally. If they
bump into (and therefore merge with) a 'train'
of their own colour that is waiting at a suitable
point on the junction, then they can continue
their journey, however the overall configuration
will now be changed irreversibly.
We could go a bit further with this process. I will not bother now!
A challenge for Bill Spight : find an elegant (diagrammatic) notation to represent these bizarre positions! :-)
Are there any Ing rules ko specialists out there who would care to prove that these positions cannot cause new problems for the Ing Rules? OK -- so that is an unkind question which does not expect a positive answer.
Are there any other types of 'zipper'?
Earlier we looked at simple splits/joints. These might be used to create various closed shapes:
|\ /\ | \ and / \ |__\ /____\An example of the first of these is:

1997/10/17 HF
Note : Both Black and White get 'stuck' when
they approach the joints -- Black at "a"
(anti-clockwise), and "d" (clockwise); White at "b"
(clockwise), and "c" (anti-clockwise). There is
an SGF version of the file
to experiment with.
Another example is:

1997/10/18 HF
and an example of the second triangle is:

1997/10/18 HF
Note: the usual restrictions on movement at
the junctions at top-left and top-right.
These are: Squares (and generally) rectangles; trapezia; rhombi (and other parallelograms).
____
| | /\
| | and / \
|____| \ /
\/
(and the related rectangles -- not shown)
The squares are illustrated in the section on 'wheels'
|\
| \
____ | \
/ \ \ \
/ \ and \ \
/________\ \___\
as well as the rhombus:
________
/ /
/ /
/_______/
(and the similar parallelograms)
which is illustrated here:
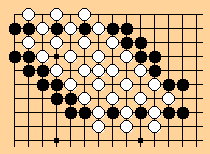
1997/10/18 HF
not to mention the hexagons:
____ _______ / \ | \ / \ | \ / \ and | \ \ / \ | \ / \ | \____/ \______|and the octagon
____
/ \
/ \
| |
| |
\ /
\____/
-- see the section on 'wheels'
We might want to include pentagons (5-sides) and heptagons (7-sides) in the above list -- both of which I expect will be easy to create if we can do all of the above. Obviously they would not be 'regular' pentagons or heptagons.
If we were determined to include all logical possibilities, we might want to include irregular shapes and polygons which were not convex -- for example the bone-shaped six-sided figure:
|\ /| | \ / | | \ / | | \/ | | | | /\ | | / \ | | / \ | |/ \|
The obvious next step is to see if we can make a zipper turn a corner, and even come back to its own origin to form a ring or 'wheel' (by analogy with the firework called a "Catherine Wheel").
It turns out that, by using (perhaps degenerate forms of) the 2 one-line zippers above, we can construct a variety of such 'wheels'.
My first creation was a 'diagonal' wheel, thus:

1996/1/30 HF
Note: The largest 'diagonal' wheel on a 19x19 board.
There is
an SGF version of the file
to experiment with.
A few months after I had discovered this (and the square wheel shown later), Theo van Ees (from Leiden, Netherlands) very kindly sent me many back-numbers of 'Go' -- the magazine of the Nederlanse Go Bond -- the Dutch Go Association. These contained numerous articles (dating from approx 1975 to 1987?) by Ger Hungerink, in which he illustrated, and discussed, some very strange, and artificial positions. Many of these can be found as "beasts" which challenge various rulesets, while some can be found among other exotic "beasts", which together contain most of these positions from his magazine articles.
Furthermore, one of
these articles (from 1975?), contains the very
same idea as in the diagram above. In volume 'Go' vol 13/4 we find:

There is an SGF version of the file to experiment with.
Some time later (1987?) Ger Hungerink published a problem, based on this idea,
in 'Go' vol 25/2:

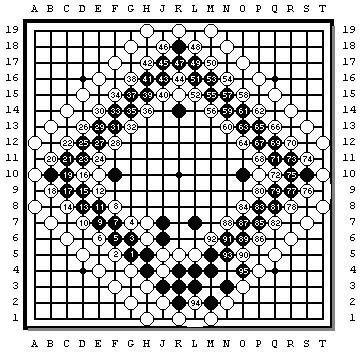
Here is an SGF version for you to play with.
A little while later (in 'Go' vol 25/4), Ger
Hungerink showed another position that is very much
the same as a wheel, and takes 100 moves to return to the original position:

Another question: how many wheels can one get
inside each other? Here is one attempt, giving two
concentric wheels:

1996/1/30 HF
Note: The largest 'diagonal' wheel, with
an additional small (not the smallest
--- see later) 'diagonal' wheel inside.
Here is
an SGF version
for you to play with.
I have not found a way to fit more than two concentric wheels onto a 19x19 Go board, although I dream that it might be possible to fit several (2 or 4) small wheels inside a large square wheel. I do not think that this is very likely, although it might be feasible to have a small diagonal wheel in the centre with a closed shape -- triangle or square -- in each of the corners.
The next to largest diagonal wheel is:

1996/2/2 HF
Obviously the 4 lots of two stones in
the middle of each side will need to
be made appropriately alive!

1996/2/8 HF
Note: The largest 'diagonal' wheel. Here is
an SGF version
for you to play with.
Note : This contains a sketch for the smallest 'diagonal' wheel inside. You should be able to see how to integrate these. :-)
A mixed wheel:
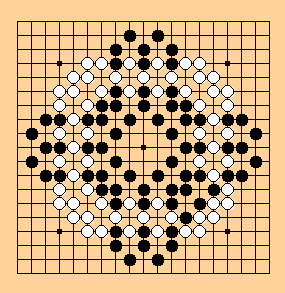
1996/2/3 HF
Note: A square wheel with diagonals
--- how else to turn the corner? Here is
an SGF version
for you to play with.
Here is the largest ('sensible' ?) square wheel:

1996/2/10 HF
Note: Sketch for a 'square' wheel. Here is an SGF version for you to play with.
Now for the smallest 'square' wheel.
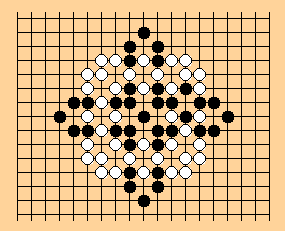
1996/05/04 HF
Note: Smallest square wheel. Here is
an SGF version
for you to play with. This position
has lots of
potential for causing problems with
the Ing Rules if we allow the outside groups
to have 'interesting' life/death status?
In early 1996 I tried hard to create such objects (on arbitrarily large boards), but with no success -- I suspected that they could not exist.
While writing up these notes in October 1997, I was lucky to make some more discoveries.
Here is a mixed 'crossing' zipper, in which a linear
zipper and a diagonal zipper cross each other.

1997/10/15 HF
Note: This is obtained by joining together a pair
of mixed two-branch zippers.
I have not been able to find non-mixed crossings -- i.e. where both are diagonal zippers, or both are linear zippers. However see the loops below.
What about cycles (which come back to their starting point), and which also cross themselves?
I call these "figure of eight" shapes 'loops'.
You might want to have several trains, or capturing segments, at the same time on each of these. Interactions (collisions) between trains become quite interesting, particularly on crossings which are restricted (one or both players may not cross freely from all branches to all other ones at a junction).
Here are some loops, including some impure forms which allow for changes of direction at the crossing point!
I will write fuller notes when time permits.

Black hubs are unconditionally alive 1997/10/15 HFThere is an SGF version to play with.
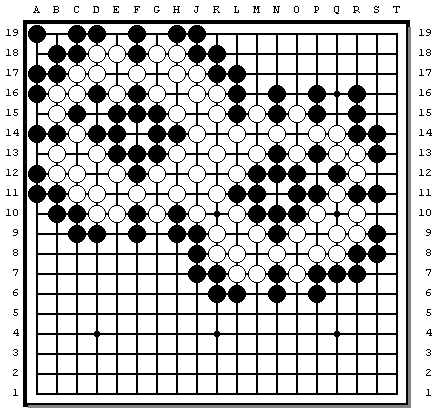
A -- a smaller loop 1997/10/15 HFThere is an SGF version to play with. Here is a slightly more compact version:

1997/10/15 HF
Please note that Black may get stuck at "a" and "b" while
going clockwise, whereas, while going anticlockwise, White
may get stuck after capturing at "c" or "d".
There is an SGF version to play with.
Here are some more shapes to create:
_______________ _______________ ______________ ______________ | | | | | | /| |\ /| | | | | | | / | | \ / | | | | | | | / | | \ / | | | | | | | / | | \ / | | | | | | | / | | \ / | |_____________| |______|______| | / | | \/ | | | | | | | / | | /\ | | | | | | | / | | / \ | | | | | | | / | | / \ | | | | | | | / | | / \ | | | | | | | / | | / \ | |_____________| |______|______| |/___________| |/__________\|and their 'diamond' versions:
/|\ /\ /\ /\ / | \ / \ / \ / \ / | \ / \ / /\ /\ /\ /___|___\ /______\ / / \ / \/ \ \ | / \ / \ / / \ /\ / \ | / \ / \/ / \/ \/ \ | / \ / \ / \ / \|/ \/ \/ \/What is the smallest board on which each of these can be made to work?
The black-and-white diagrams were produced from the screen display of the WinMGT program.
Last Updated 2000/09/13
This page maintained by Harry@goban.demon.co.uk.NOSPAM (sorry please remove ".NOSPAM" from my address), whose WWW page is Harry Fearnley's Home Page